10. Rewards
Defining a reward function is essential in reinforcement learning. As such, Sinergym provides the option to use pre-implemented reward functions or define custom ones (refer to the section below).
Sinergym’s predefined reward functions are designed as multi-objective, incorporating both energy consumption and thermal discomfort. These are normalized and combined with varying weights. These rewards are always negative, signifying that optimal behavior results in a cumulative reward of 0. Separate temperature comfort ranges are defined for summer and winter periods. The weights assigned to each term in the reward function allow for adjusting the importance of each aspect during environment evaluation.
The core concept of the reward system in Sinergym is encapsulated by the following equation:
Where:
\(P_t\) represents power consumption,
\(T_t\) is the current indoor temperature,
\(T_{up}\) and \(T_{low}\) are the upper and lower comfort range limits, respectively,
\(\omega\) is the weight assigned to power consumption, and consequently, \(1 - \omega\) represents the comfort weight,
\(\lambda_P\) and \(\lambda_T\) are scaling constants for consumption and comfort penalties, respectively.
Warning
The constants \(\lambda_P\) and \(\lambda_T\) are configured to create a proportional relationship between energy and comfort penalties, calibrating their magnitudes. When working with different buildings, it’s crucial to adjust these constants to maintain a similar magnitude of the reward components.
Different types of reward functions are designed based on specific details:
LinearRewardimplements a linear reward function, where discomfort is calculated as the absolute difference between the current temperature and the comfort range.ExpRewardis similar to the linear reward, but calculates discomfort using the exponential difference between the current temperature and comfort ranges, resulting in a higher penalty for larger deviations from target temperatures.HourlyLinearRewardadjusts the weight assigned to discomfort based on the hour of the day, emphasizing energy consumption outside working hours more.NormalizedLinearRewardnormalizes the reward components based on the maximum energy penalty and comfort penalty, providing adaptability during the simulation. In this reward, the \(\lambda_P\) and \(\lambda_T\) constants are not required to calibrate both magnitudes.
Warning
This reward function is not very precise at the beginning of the simulation, be careful with that.
These reward functions have parameters in their constructors, the values of which may vary based on the building
used or other factors. By default, all environments use the LinearReward with default parameters for each
building. To change this, refer to the example in Adding a new reward.
Warning
When specifying a reward different from the default environment ID with gym.make, it’s crucial to set the reward_kwargs that are required and thus don’t have a default value.
10.1. Reward terms
By default, reward functions return the reward scalar value and the terms used in their calculation. The values of these terms depend on the specific reward function used and are automatically added to the environment’s info dictionary. The structure typically matches the diagram below:
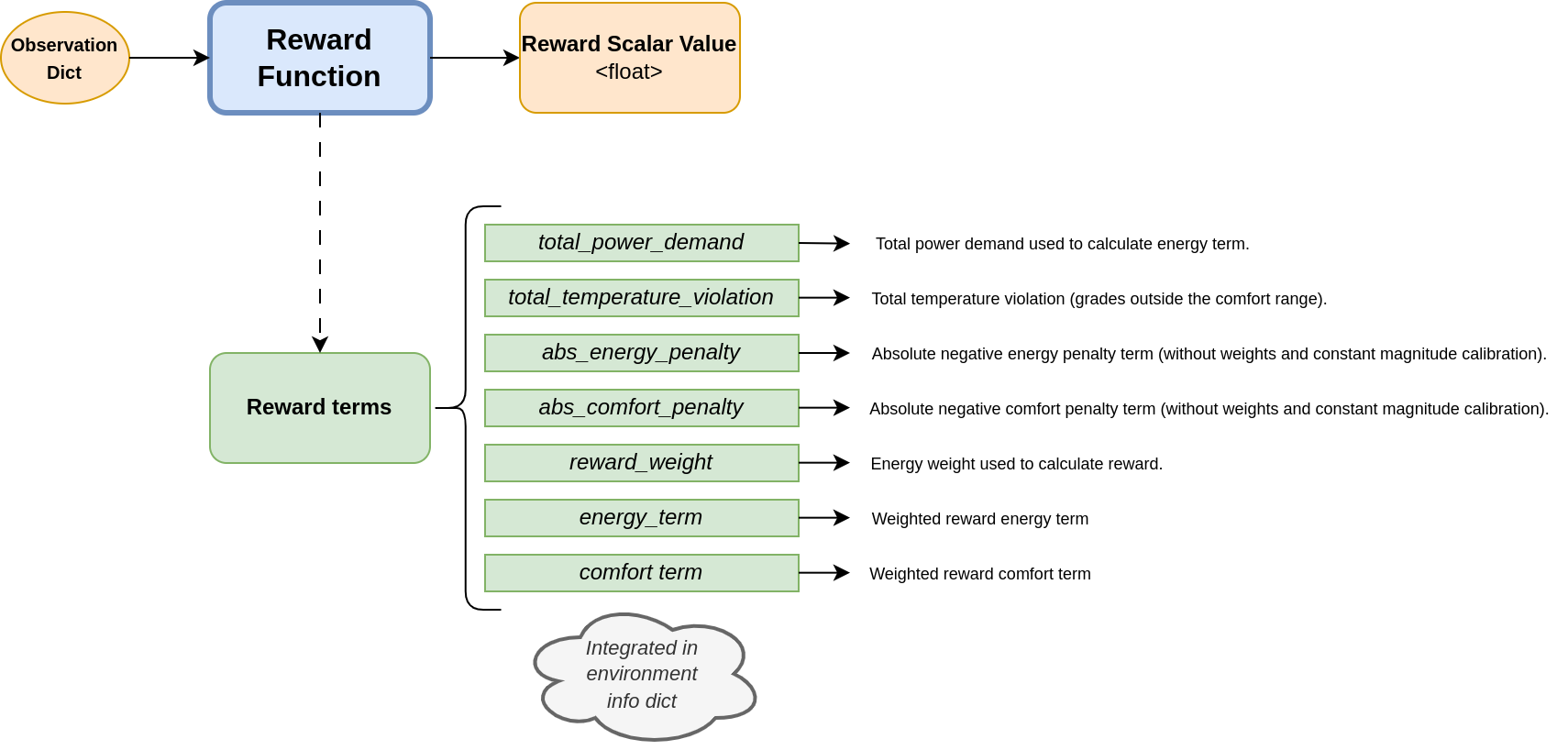
10.2. Custom Rewards
Defining custom reward functions is also straightforward. For instance, a reward signal that always returns -1 can be implemented as shown:
from sinergym.utils.rewards import BaseReward
class CustomReward(BaseReward):
"""Naive reward function."""
def __init__(self, env):
super(CustomReward, self).__init__(env)
def __call__(self, obs_dict):
return -1.0, {}
env = gym.make('Eplus-discrete-stochastic-mixed-v1', reward=CustomReward)
For advanced reward functions, we recommend inheriting from our main class, LinearReward,
and overriding relevant methods. Our reward functions simplify observation processing to
extract consumption and comfort violation data, from which absolute penalty values are calculated.
Weighted reward terms are then calculated from these penalties and summed.
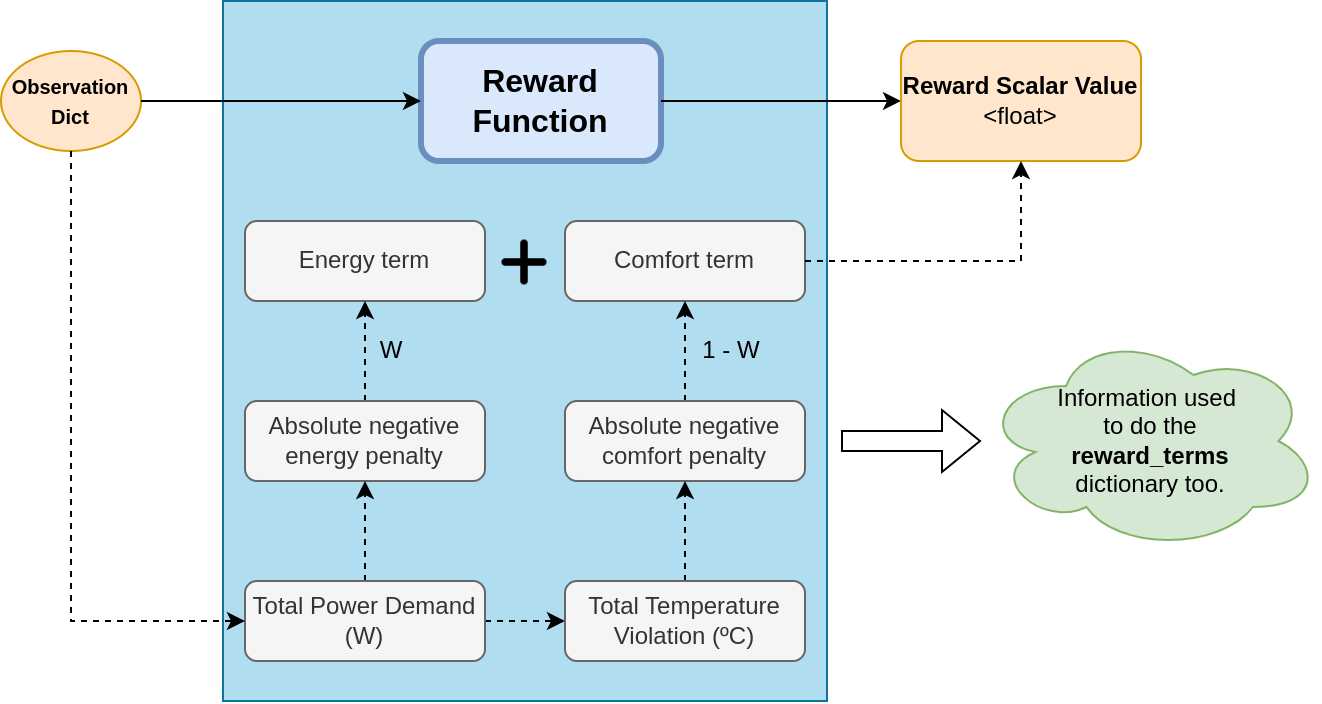
By modularizing each of these steps, you can quickly and easily modify specific aspects of the reward to create a new one, as demonstrated with our exponential function reward version, for example.
More reward functions will be included in the future, so stay tuned!